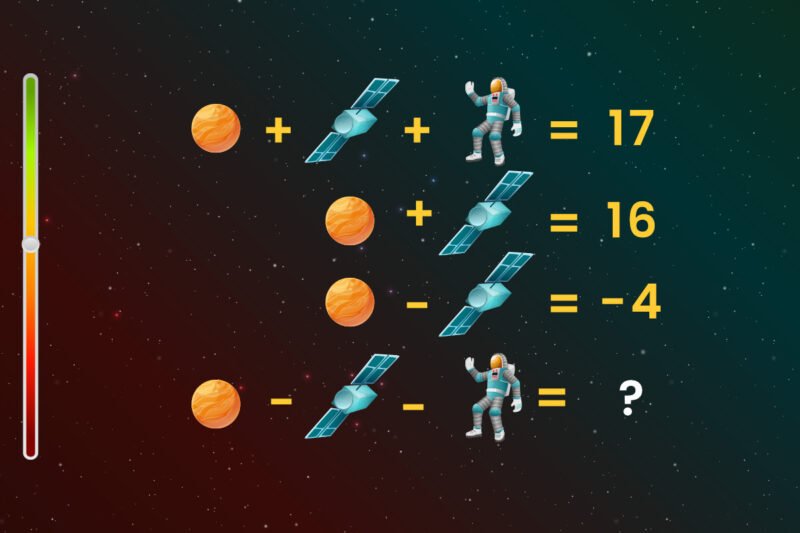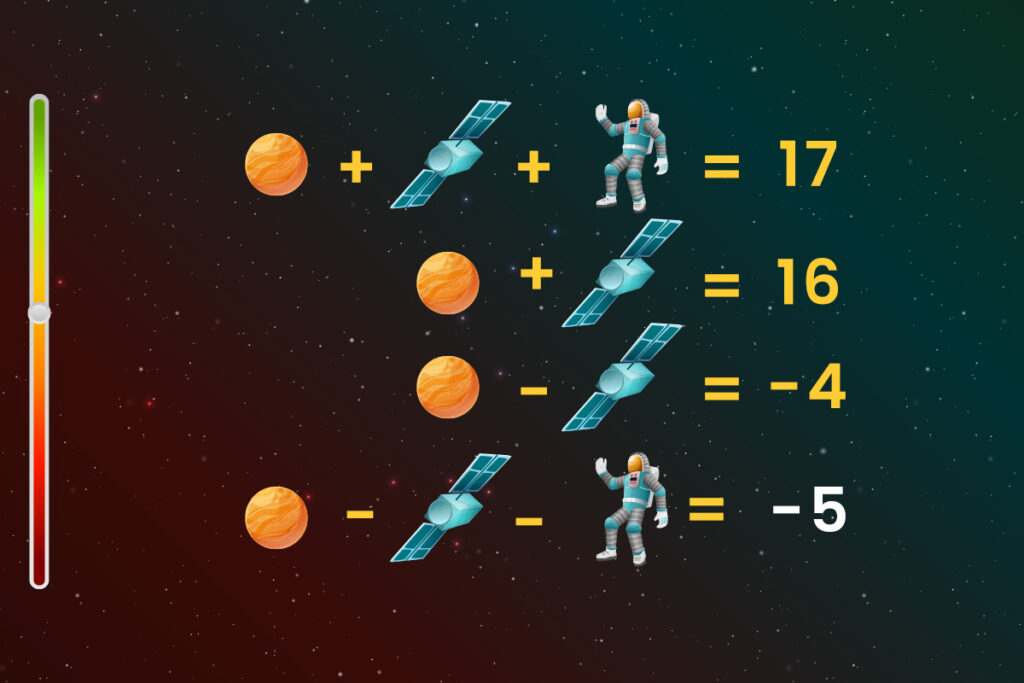Hello everyone puzzle lovers, maths freaks and fans of complex solutions! Today we’re giving you a challenge that will put your logic, deductive skills and creativity to the test.
Get ready to dive into an unusual mathematical puzzle that will leave you baffled. You’re going to have to rack your brains and hold on tight, because the solution to this puzzle is not as obvious as it might seem.
You thought you’d mastered calculations and equations? Well, think again! This puzzle is a veritable maze of interwoven enigmas, ready to trap you at every turn. Are you up to the challenge?
So get ready, because you’re about to enter an enigmatic mathematical universe where only the brightest will be able to solve this mind-boggling mystery. Are you ready to play with numbers and defy the laws of logic? If so, follow us through this mathematical maze and prove that you have the genius to solve this intriguing enigma.
The intriguing mathematical challenge
In this unusual maths puzzle, you’ll be faced with an intriguing brainteaser that will put your thinking to the test. The challenge consists of a series of equations in which you have to find the missing value.
Here are the different equations that make up the puzzle:
- First equation: 6 + 10 + 1 = 17
- Second equation: 6 + 10 = 16
- Third equation: 6 – 10 = ?
- Fourth equation: 6 – 10 – 1 = ?
Each of these equations is unique and will test your ability to find the missing solution. If you’re up to this mathematical challenge, read on to find out how to tackle this puzzle step by step.
The solutions to the unusual mathematical puzzle :
- First equation: 6 + 10 + 1 = 17
- Second equation: 6 + 10 = 16
- Third equation: 6 – 10 = -4
- Fourth equation: 6 – 10 – 1 = -5
Explanation of the solution:
In the first equation, we successively add the numbers 6, 10 and 1, which gives 17 as the result.
In the second equation, we add the numbers 6 and 10, giving 16 as the result.
In the third equation, we subtract the number 10 from 6, which gives a result of -4. When a larger number is subtracted from a smaller number, the result is always negative.
In the fourth equation, the numbers 10 and 1 are successively subtracted from 6, giving a result of -5.
So we’ve found the solutions to each of the equations presented in this unusual mathematical puzzle.