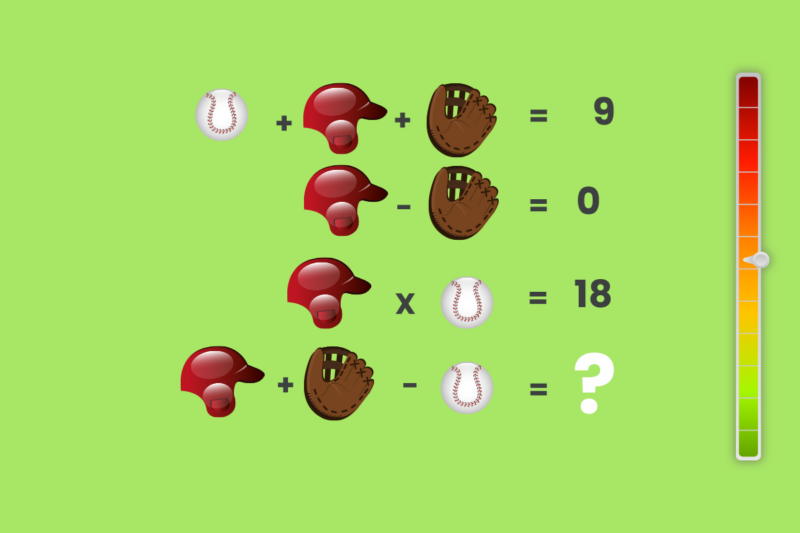Imagine yourself plunged into a mysterious universe where numbers and equations come to life to baffle your mind and challenge your logical abilities. A mathematical riddle that seems impossible to solve, that will put your perspicacity to the test and shake your confidence in your own faculties.
Will you dare to enter this thrilling mental game where reality and fiction merge? Expect a disconcerting experience a challenge that will make you question everything you thought you knew about mathematics.
Get ready to plunge into the abyss of this incredibly complex puzzle and let yourself be swept away by the suspense and excitement that awaits you. Are you ready to take part in this captivating adventure where the possible and the impossible meet?
The Mathematical Enigma of the Impossible
Imagine a mathematical riddle so complex, so intriguing that it seems impossible to solve. It’s a challenge that has the power to stimulate the brightest minds while perplexing the rest. The stakes are high for those who dare to try it, because the solution promises to reveal an elusive mathematical mystery.
The equations involved are as follows:
– Baseball + Helmet + Glove = 9
– Helmet – Glove = 0
– Helmet x Baseball = 18
– Helmet + Glove – Baseball = ?
These equations are like pieces of a jigsaw puzzle, apparently contradictory but intimately linked. How can they fit together to form a coherent solution? Therein lies the challenge, therein lies the ultimate exhilaration of solving this mathematical riddle of the impossible. So, will you dare to take up this intellectual challenge?
The Solution to the Mathematical Enigma
The solution to the given problem is that Helmet = 3, Baseball = 6 and Glove = 3. Replacing these values in the equations gives :
– Baseball + Helmet + Glove = 6 + 3 + 3 = 9
– Helmet – Glove = 3 – 3 = 0
– Helmet x Baseball = 3 x 6 = 18
– Helmet + Glove – Baseball = 3 + 3 – 6 = 6
The equations are solved using arithmetic and substituting the appropriate values for each variable.
In this way, the values of helmet, baseball and glove can be determined, forming a coherent solution to the seemingly impossible mathematical puzzle.
This demonstrates the importance of thorough analysis of equations and finding relationships between variables.